About / 关于 Archive / 归档 Categories / 分类 Tags / 标签 Friends / 友链 RSS
- 目录 -
POI2007 选做
folder OI 题解   schedule 18 min 45 s.

P3453 Drz-Trees

简要题意: 给定序列 $h_{1\cdots n}$，定义其权值为 $\sum_{i=1}^{n-1} |h_i-h_{i+1}|$。对于每个 $i$，求出将 $h_i$ 与另一个 $h_j$ 交换后（可以不交换），序列权值的最小值。

数据规模: $n \le 5\times 10^4,\ 1\le h_i \le 10^8$。

题解: 方便起见，定义 $mx_i = \max(h_{i-1},h_{i+1}),\ mn_i = \min(h_{i-1},h_{i+1}),\ val_i = |h_i-mn_i| + |h_i-mx_i|$。

考虑交换两个数 $i$ 和 $j$ 后对答案的贡献，先只讨论一般的情况，即 $i,j \notin \{1,n\}$ 且 $|i-j| \neq 1$。注意到此时的贡献即为 $-val_i - val_j + |h_i-mn_j| + |h_i-mx_j| + |h_j - mn_i| + |h_j - mx_i|$。

由于求的是最小权值，所以必须分情况讨论拆掉绝对值。即对于 $h_i$，与 $mn_j,mx_j$ 的大小情况有 $3$ 种，对于 $h_j$ 同理，共 $9$ 种情况。此时 $i$ 和 $j$ 对答案的贡献独立，不妨设为 $f(i)$ 和 $f(j)$。

下面讨论更一般的情况，即对于 $h_i$ 需要满足 $l_j \le h_i \le r_j$，对 $h_j$ 需要满足 $l_i \le h_j \le r_i$，求 $\min(f(i) + f(j))$。将 $i$ 的限制看作 $(h_i,l_i)\sim (h_i,r_i)$ 的线段，$j$ 的限制看作 $(l_j,h_j)\sim (r_j,h_j)$ 的线段，若两条线段有交，则对答案能够产生贡献。于是可以使用扫描线，将 $h_i$ 离散化并且使得每个 $h_i$ 都对应一个位置（也就是只排序不去重），$j$ 所加入的线段在两个端点处覆盖线段树叶子结点的值（这样可以在维护 $\min$ 时进行删除操作），在 $i$ 处查询区间 $\min$ 即可。注意此时需要保证 $|i-j| \neq 1$，否则贡献不对，只需要在 $i$ 处查询时的区间中剔除 $h_{i-1}$ 和 $h_{i+1}$ 即可。

最后再讨论 $i=1,\ i=n,\ |i-j|=1$ 的特殊情况即可，容易发现可以直接枚举并简单计算。于是本题在 $O(n\log n)$ 的时间复杂度内解决，有 $9$ 倍的常数。

代码的实现，发现其他人写的都非常长，其实可以将扫描线的部分封装一下，极大地减少代码量。我在封装扫描线的时候采用了函数作为传参，个人认为写的比较优雅。其实也可以在扫描线之前就用数组存好对应的区间以及贡献。下面的代码在采用空格缩进的情况下只有 $5\text{KB}$ 不到，可以作为参考。

代码:

C++
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129

using ll = long long;
using func = function<int(int)>;
const int N = 5e4 + 10, I = 1e9 + 10;
int n, h[N], id[N], mp[N], mx[N], mn[N], val[N], rgl[N][3], rgr[N][3];
ll ans[N], sans;
vector<pair<int, int>> vec[N];
template <class _Tx, class _Ty> inline void chkmin(_Tx &x, _Ty y) {
  x > y && (x = y);
}
inline int dif(int x, int y) {
  if (x < 1 || y > n)
    return 0;
  return abs(mp[h[x]] - mp[h[y]]);
}
struct Info {
  func li, ri, fi, lj, rj, fj;
  Info(func li, func ri, func fi, func lj, func rj, func fj)
      : li(li), ri(ri), fi(fi), lj(lj), rj(rj), fj(fj) {}
};
struct SegmentTree {
  int mn[N * 4];
  inline int ls(int p) { return p << 1; }
  inline int rs(int p) { return p << 1 | 1; }
  void build(int i, int l, int r) {
    mn[i] = I;
    if (l == r)
      return;
    int mid = (l + r) >> 1;
    build(ls(i), l, mid), build(rs(i), mid + 1, r);
  }
  void update(int i, int l, int r, int p, int v) {
    if (l == r)
      return mn[i] = v, void();
    int mid = (l + r) >> 1;
    p <= mid ? update(ls(i), l, mid, p, v) : update(rs(i), mid + 1, r, p, v);
    mn[i] = min(mn[ls(i)], mn[rs(i)]);
  }
  int query(int i, int l, int r, int ql, int qr) {
    if (ql > qr)
      return I;
    if (ql <= l && r <= qr)
      return mn[i];
    int mid = (l + r) >> 1, ret = I;
    if (ql <= mid)
      ret = min(ret, query(ls(i), l, mid, ql, qr));
    if (qr > mid)
      ret = min(ret, query(rs(i), mid + 1, r, ql, qr));
    return ret;
  }
} sgt;
ll calc(int x, int y) {
  if (x + 1 == y) {
    return dif(x - 1, y) + dif(x, y + 1) - dif(x - 1, x) - dif(y, y + 1);
  } else {
    return dif(x - 1, y) + dif(y, x + 1) - dif(x - 1, x) - dif(x, x + 1) +
           dif(y - 1, x) + dif(x, y + 1) - dif(y - 1, y) - dif(y, y + 1);
  }
}
ll query(int p, int l, int r) {
  int x, y;
  ll ret = 1e18;
  tie(x, y) = minmax(h[p - 1], h[p + 1]);
  chkmin(ret, sgt.query(1, 1, n, l, min(r, x - 1)));
  chkmin(ret, sgt.query(1, 1, n, max(l, x + 1), min(r, y - 1)));
  chkmin(ret, sgt.query(1, 1, n, max(l, y + 1), r));
  return ret;
}
void solve(const Info &info) {
  for (int i = 1; i <= n + 1; ++i)
    vec[i].clear();
  for (int i = 2; i < n; ++i) {
    vec[info.lj(i)].push_back({h[i], info.fj(i)});
    vec[info.rj(i) + 1].push_back({h[i], I});
  }
  sgt.build(1, 1, n);
  for (int i = 1; i <= n; ++i) {
    int k = id[i];
    for (auto p : vec[i])
      sgt.update(1, 1, n, p.first, p.second);
    if (k == 1 || k == n)
      continue;
    chkmin(ans[k], query(k, info.li(k), info.ri(k)) + info.fi(k));
  }
}
signed main() {
  ios::sync_with_stdio(false);
  cin.tie(nullptr), cout.tie(nullptr);
  cin >> n;
  for (int i = 1; i <= n; ++i)
    cin >> h[i];
  iota(id + 1, id + n + 1, 1);
  sort(id + 1, id + n + 1, [&](int x, int y) { return h[x] < h[y]; });
  for (int i = 1; i <= n; ++i)
    mp[i] = h[id[i]], h[id[i]] = i;
  for (int i = 1; i <= n; ++i) {
    mx[i] = max(h[i - 1], h[i + 1]);
    mn[i] = min(h[i - 1], h[i + 1]);
    rgl[i][0] = 1, rgl[i][1] = mn[i], rgl[i][2] = mx[i];
    rgr[i][0] = mn[i], rgr[i][1] = mx[i], rgr[i][2] = n;
    val[i] = dif(i - 1, i) + dif(i, i + 1), sans += dif(i - 1, i);
  }
  const array<int, 3> coef_h = {-2, 0, 2}, coef_mx = {1, 1, -1},
                      coef_mn = {1, -1, -1};
  for (int i = 0; i < 3; ++i)
    for (int j = 0; j < 3; ++j) {
      auto li = [&](int id) { return rgl[id][j]; };
      auto ri = [&](int id) { return rgr[id][j]; };
      auto fi = [&](int id) {
        return -val[id] + coef_h[i] * mp[h[id]] + coef_mx[j] * mp[mx[id]] +
               coef_mn[j] * mp[mn[id]];
      };
      auto lj = [&](int id) { return rgl[id][i]; };
      auto rj = [&](int id) { return rgr[id][i]; };
      auto fj = [&](int id) {
        return -val[id] + coef_h[j] * mp[h[id]] + coef_mx[i] * mp[mx[id]] +
               coef_mn[i] * mp[mn[id]];
      };
      solve(Info(li, ri, fi, lj, rj, fj));
    }
  for (int i = 1; i <= n; ++i)
    chkmin(ans[1], calc(1, i)), chkmin(ans[i], calc(1, i));
  for (int i = 1; i <= n; ++i)
    chkmin(ans[n], calc(i, n)), chkmin(ans[i], calc(i, n));
  for (int i = 2; i <= n; ++i)
    chkmin(ans[i - 1], calc(i - 1, i)), chkmin(ans[i], calc(i - 1, i));
  for (int i = 1; i <= n; ++i)
    cout << sans + ans[i] << "\n";
  return 0;
}

P3454 Osi-Axes of Symmetry

简要题意: 求给定的简单多边形的对称轴数量，多边形不一定是凸的。有多组数据。

数据规模: $n \le 10^5,\ |x_i|,|y_i| \le 10^8$。

题解: 考虑枚举对称轴的一个点 $P$，容易维护出其对面的点 $Q$，考虑判定直线 $PQ$ 是否为多边形的对称轴，即判断 $P\to Q$ 的两条路径是否对称。一个套路的做法就是按顺序维护边长的平方以及角度的叉积，判断时直接判断是否是回文即可，用 hash 或 manacher 均可。

注意对称轴有可能会与多边形的某条边垂直，但此时仍然是一个奇回文串，不需要特殊考虑。

代码:

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

using ll = long long;
const int N = 4e5 + 10;
int n, m, ans, d[N];
ll str[N];
bool chk[N];
inline int pre(int x, int n) { return x == 1 ? n : x - 1; }
inline int nxt(int x, int n) { return x == n ? 1 : x + 1; }
struct Point {
  int x, y;
  Point operator-(const Point &p) const { return {x - p.x, y - p.y}; }
  ll operator*(const Point &p) const { return 1ll * x * p.y - 1ll * y * p.x; }
  ll dist() const { return 1ll * x * x + 1ll * y * y; }
} pt[N];
signed main() {
  int cas;
  read(cas);
  while (cas--) {
    read(n), m = 0, ans = 0;
    fill(chk + 1, chk + n + n + 1, 0);
    for (int i = 1; i <= n; ++i)
      read(pt[i].x), read(pt[i].y);
    for (int i = 1; i <= n; ++i) {
      int p1 = pre(i, n), p2 = nxt(i, n);
      str[++m] = (pt[p2] - pt[i]) * (pt[i] - pt[p1]);
      str[++m] = (pt[p2] - pt[i]).dist();
    }
    copy(str + 1, str + m + 1, str + m + 1), m <<= 1;
    for (int i = 1, mx = 0, id = 0; i <= m; ++i) {
      d[i] = (i <= mx) ? min(mx - i + 1, d[id * 2 - i]) : 1;
      while (str[i - d[i]] == str[i + d[i]])
        ++d[i];
      if (i + d[i] - 1 > mx)
        mx = i + d[i] - 1, id = i;
      if (i <= n * 2 && d[i] >= n)
        chk[i % (n + n)] = 1;
    }
    for (int i = 1; i <= n + n; ++i)
      ans += chk[i];
    write(ans), putchar('\n');
  }
  return 0;
}

P3455 Zap-Queries

简要题意: 有 $n$ 组询问，每次询问给定 $a,b,d$，求 $\sum\limits_{x=1}^{a}\sum\limits_{y=1}^{b}[\gcd(x,y)=d]$。

数据规模: $n,a,b,d \le 5\times 10^4$。

题解: 莫反+数论分块板子题。直接推式子：

$$ \begin{aligned} &\sum_{x=1}^{a}\sum_{y=1}^{b}[\gcd(x,y) = d] \\ =& \sum_{x=1}^{a/d}\sum_{y=1}^{b/d}[\gcd(x,y)=1] \\ =& \sum_{i=1}^{\min(a/d,b/d)}\mu(i)\lfloor\frac{a}{di}\rfloor\lfloor\frac{b}{di}\rfloor \end{aligned} $$

对后面的向下取整分别求出数论分块的区间硬做就行，复杂度为 $O(n(\sqrt \frac{a}{d} + \sqrt \frac{b}{d}))$。

代码:

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

using ll = long long;
const int N = 5e4 + 10;
int n, a, b, d, cntp, pri[N], miu[N], smiu[N];
bool mark[N];
void sieve(int n) {
  mark[1] = miu[1] = smiu[1] = 1;
  for (int i = 2; i <= n; ++i) {
    if (!mark[i])
      pri[++cntp] = i, miu[i] = -1;
    for (int j = 1; j <= cntp; ++j) {
      if (i * pri[j] > n)
        break;
      mark[i * pri[j]] = 1;
      if (i % pri[j] == 0) {
        miu[i * pri[j]] = 0;
        break;
      }
      miu[i * pri[j]] = -miu[i];
    }
    smiu[i] = smiu[i - 1] + miu[i];
  }
}
signed main() {
  read(n), sieve(5e4);
  while (n--) {
    int ans = 0;
    read(a), read(b), read(d);
    if ((a /= d) > (b /= d))
      swap(a, b);
    for (int l = 1, r; l <= a; l = r + 1) {
      r = min(a / (a / l), b / (b / l));
      ans += (smiu[r] - smiu[l - 1]) * (a / l) * (b / l);
    }
    write(ans), putchar('\n');
  }
  return 0;
}

P3457 Pow-The Flood

简要题意: 给定一张 $n\times m$ 的地势图，所有的点都被水淹没，现在有一些关键点，要求放最少的水泵使所有关键点的水都被抽干。

数据规模: $n,m \le 10^3$。

题解: 根据连通器原理，我们知道点 $p$ 能被抽干，当且仅当存在一个点 $q$ 有水泵，且存在至少一条 $p$ 到 $q$ 的路径不经过高度 $> height_p$ 的点。于是可以按照海拔高度从小到大加入每个点，用并查集维护连通块中是否存在水泵。

P3458 Ska-Rock Garden

简要题意: 有平面上若干个点，点 $(x,y)$ 可以移动到 $(y,x)$，代价为 $w_i$。求包含所有点的矩形的最小周长，以及在周长最小的情况下花费的最小代价，并输出移动方案。

数据规模: $n \le 10^6,\ 0 \le x_i,y_i \le 10^9$。

题解: $(x,y)$ 变换到 $(y,x)$，相当于沿对角线 $y=x$ 翻折。可以发现，若将所有点翻折到对角线的同一侧，周长一定不会变差，证明可以考虑下面两张图（图片来自洛谷上的第二篇题解）：

img1

img2

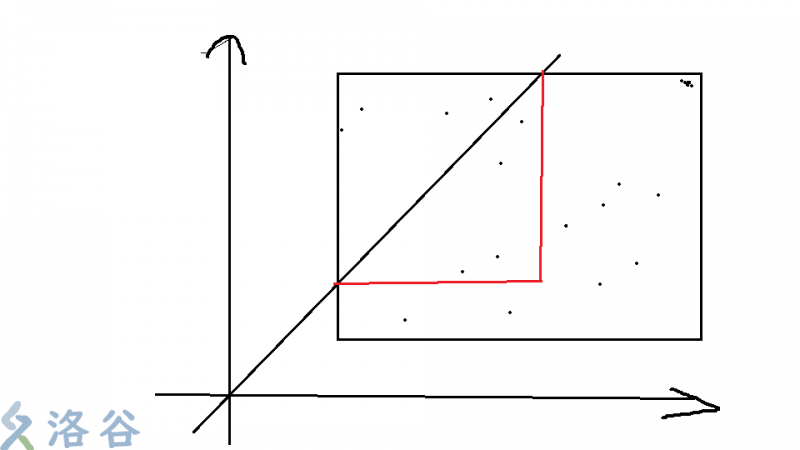
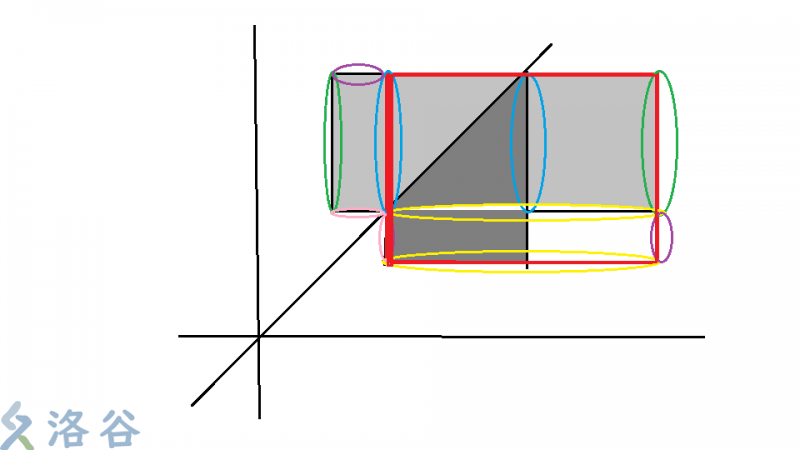
于是就可以确定出最终的周长以及坐标的范围，分 $4$ 种情况讨论下即可。

代码:

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63

using ll = long long;
const int N = 1e6 + 10;
int n, px[N], py[N], tx[N], ty[N], wt[N];
bool use1[N], use2[N];
using result = tuple<ll, int, bitset<N>>;
inline bool operator<(const bitset<N> &x, const bitset<N> &y) {
  for (int i = 0; i < N; ++i)
    if (x[i] != y[i])
      return x[i] < y[i];
  return false;
}
inline bool operator<(const result &x, const result &y) {
  if (get<0>(x) != get<0>(y))
    return get<0>(x) < get<0>(y);
  if (get<1>(x) != get<1>(y))
    return get<1>(x) < get<1>(y);
  if (get<2>(x) != get<2>(y))
    return get<2>(x) < get<2>(y);
  return false;
}
inline void chkmin(result &x, result y) {
  if (y < x)
    x = y;
}
result calc(int xmn, int xmx, int ymn, int ymx) {
  int sum = 0;
  bitset<N> use;
  ll ans = 2ll * (xmx - xmn + ymx - ymn);
  for (int i = 1; i <= n; ++i) {
    if (xmn <= px[i] && px[i] <= xmx && ymn <= py[i] && py[i] <= ymx) {
      use[i] = 0;
    } else if (xmn <= py[i] && py[i] <= xmx && ymn <= px[i] && px[i] <= ymx) {
      use[i] = 1, sum += wt[i];
    } else {
      return make_tuple((ll)1e18, (int)1e9, bitset<N>(0));
    }
  }
  return make_tuple(ans, sum, use);
}
signed main() {
  read(n);
  for (int i = 1; i <= n; ++i)
    read(px[i]), read(py[i]), read(wt[i]);
  for (int i = 1; i <= n; ++i)
    if (px[i] < py[i]) {
      tie(tx[i], ty[i]) = make_tuple(py[i], px[i]);
    } else {
      tie(tx[i], ty[i]) = make_tuple(px[i], py[i]);
    }
  int xmx = *max_element(tx + 1, tx + n + 1),
      xmn = *min_element(tx + 1, tx + n + 1);
  int ymx = *max_element(ty + 1, ty + n + 1),
      ymn = *min_element(ty + 1, ty + n + 1);
  result res = {(ll)1e18, (int)1e9, bitset<N>(0)};
  chkmin(res, calc(xmn, xmx, ymn, ymx));
  chkmin(res, calc(xmn, ymx, ymn, xmx));
  chkmin(res, calc(ymn, xmx, xmn, ymx));
  chkmin(res, calc(ymn, ymx, xmn, xmx));
  printf("%lld %d\n", get<0>(res), get<1>(res));
  for (int i = 1; i <= n; ++i)
    putchar("01"[get<2>(res)[i]]);
  return putchar('\n'), 0;
}

P3459 Meg-Megalopolis

简要题意: 给一棵树，初始边权为 $1$，$m$ 次操作或询问，将 $(u,v) \in E$ 的边权设为 $0$，或查询根到 $u$ 的距离。

数据规模: $n, m \le 2.5 \times 10^5$。

题解: 没有技术含量的，发现每次操作即将某个子树的答案 $-1$，直接在 dfs 序上用线段树维护。

P6564 Klo-堆积木

简要题意: 给定长度为 $n$ 的数组 $a$，求权值最大的子序列 $a_{b_1} \cdots a_{b_k}$，权值为 $\sum_{i=1}^{k}[a_{b_i}=i]$。

数据规模: $n \le 10^5,\ a_i \le 10^6$。

题解: 先考虑 dp，$dp_i$ 表示以 $i$ 结尾的子序列的最大权值。最暴力的做法是枚举前驱状态转移，$O(n^2)$ 无法通过。

思考什么情况下 $dp_j$ 能够转移到 $dp_i$，不难得出要同时满足以下条件：

$$ \begin{cases} \begin{aligned} i &> j & (1) \\ a_i &> a_j & (2) \\ i - a_i &\ge j - a_j &(3) \\ \end{aligned} \end{cases} $$

同时注意到，当条件 $(2)$ 和 $(3)$ 同时满足时，条件 $(1)$ 也就能够满足。于是题目转化为对 $(a_i, i - a_i)$ 的二维偏序问题，用树状数组或 CDQ 分治解决即可。

代码: (学校 OJ 上要输出方案，而洛谷输出的是权值，略有不同)。

C++
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

using ll = long long;
using pii = pair<int, int>;
const int N = 1e5 + 10;
int n, a[N], id[N], dp[N], pre[N];
bool vis[N];
pii bit[N];
inline void chkmax(pii &x, pii y) {
  if (x < y)
    x = y;
}
void add(int x, pii v) {
  if (x <= 0)
    return;
  for (int i = x; i <= n; i += i & -i)
    chkmax(bit[i], v);
}
pii sum(int x) {
  pii ret(0, 0);
  for (int i = x; i; i -= i & -i)
    chkmax(ret, bit[i]);
  return ret;
}
signed main() {
  read(n);
  for (int i = 1; i <= n; ++i)
    read(a[i]);
  iota(id + 1, id + n + 1, 1);
  sort(id + 1, id + n + 1, [&](int x, int y) { return a[x] < a[y]; });
  for (int i = 1, p = 0; i <= n; ++i) {
    if (a[id[i]] > id[i])
      continue;
    while (p <= n && a[id[p]] < a[id[i]])
      add(id[p] - a[id[p]] + 1, make_pair(dp[id[p]], id[p])), ++p;
    tie(dp[id[i]], pre[id[i]]) = sum(id[i] - a[id[i]] + 1), ++dp[id[i]];
  }
  vector<int> vec;
  int pos = max_element(dp + 1, dp + n + 1) - dp;
  // write(dp[pos]), putchar('\n');
  while (pos) {
    for (int i = 0; i < a[pos] - a[pre[pos]]; ++i)
      vis[pos - i] = 1;
    pos = pre[pos];
  }
  for (int i = 1; i <= n; ++i)
    if (!vis[i])
      vec.push_back(i);
  write(vec.size()), putchar('\n');
  for (int i = 0; i < (int)vec.size(); ++i)
    write(vec[i]), putchar(" \n"[i == (int)vec.size() - 1]);
  return 0;
}

最后修改于 2025-07-05

Git 版本: de2abab

yaoxi-std 的博客
About / 关于 Archive / 归档 Categories / 分类 Tags / 标签 Friends / 友链 RSS
Hugo Theme Diary by Rise
移植自 Makito's Journal.

© yaoxi-std, CC BY-NC-SA 4.0 Licensed
- 目录 -