P3418 Pun
简要题意: 给定模式点集和其他若干个点集,判断每个点集是否和模式点集相似。
数据规模: 点集大小 $n \le 25,000$,点集数量 $k \le 20$。
题解: 首先考虑消除题面中的 $4$ 种变换,即 平移、旋转、翻转和缩放。
平移的消除类似无序运动这道题,但现在给定的点之间没有了相对顺序,也就无法像那道题一样取运动的开始点作为基准点。因此,我们需要找到一个新的基准点,使得无论这组点集如何进行线性变换,它和其他点的相对位置都不会改变。不难发现可以取整个点集的重心,即 $(\frac{1}{n}\sum x,\frac{1}{n}\sum y)$ 。将点集的重心移动到坐标原点,以方便后续的计算。
接下来考虑缩放。注意到缩放只是对坐标轴上单位 $1$ 的改变,因此只需要对点集确定一个独一无二的长度作为单位 $1$ 即可。到原点距离的 $\max / \min$ 均可,实现上也差别不大。
对于旋转操作,首先想到的便是对点集进行极角排序,对于极角相同的按照到原点的距离排序。但是当点集旋转时,极角的大小会进行改变,甚至连相对位置都变了。但注意到排序之后,相邻两个极角的差分值一定不会改变,故只需要记录极角的差分值即可。对了,还要注意特判有点刚好在原点上的情况,这个点的极角是不存在的。
至于翻转操作,其实是最简单的,只需将 $x$ 轴或 $y$ 轴的任意一个翻转再匹配一遍即可。
匹配时,由于旋转的角度不确定,所以破环为链跑 kmp 即可。复杂度 $O(nk)$,常数比较大。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
bool m_be;
using ll = long long;
using ld = double;
const int N = 3e4 + 10;
const ld eps = 1e-10;
int q;
inline int cmp(const ld &x) {
if (abs(x) < eps)
return 0;
return x < 0 ? -1 : 1;
}
inline bool equ(const pair<ld, ld> &x, const pair<ld, ld> &y) {
return !cmp(x.first - y.first) && !cmp(x.second - y.second);
}
struct Point {
ld x, y;
Point operator+(const Point &p) const { return {x + p.x, y + p.y}; }
Point operator-(const Point &p) const { return {x - p.x, y - p.y}; }
Point operator*(const ld &k) const { return {x * k, y * k}; }
Point operator/(const ld &k) const { return {x / k, y / k}; }
bool operator==(const Point &p) const {
return !cmp(x - p.x) && !cmp(y - p.y);
}
ld dist() const { return hypot(x, y); }
ld angle() const { return atan2(y, x); }
};
struct Points {
int n;
bool onf;
Point pt[N];
pair<ld, ld> s1[N], s2[N];
int kmp1[N], kmp2[N];
void input(bool flag) {
read(n), onf = false;
for (int i = 1; i <= n; ++i)
read(pt[i].x), read(pt[i].y);
Point foc = accumulate(pt + 1, pt + n + 1, Point{0, 0}) / n;
for (int i = 1; i <= n; ++i)
pt[i] = pt[i] - foc;
for (int i = 1; i <= n; ++i)
if (pt[i] == Point{0, 0})
swap(pt[i--], pt[n--]), onf = true;
ld mxd = 0;
for (int i = 1; i <= n; ++i)
mxd = max(mxd, pt[i].dist());
for (int i = 1; i <= n; ++i)
pt[i] = pt[i] / mxd;
sort(pt + 1, pt + n + 1,
[](const Point &p1, const Point &p2) {
ld k1 = p1.angle(), k2 = p2.angle();
return cmp(k1 - k2) ? k1 < k2 : p1.dist() < p2.dist();
}),
build(s1);
if (!flag)
return;
for (int i = 1; i <= n; ++i)
pt[i].x *= -1;
sort(pt + 1, pt + n + 1,
[](const Point &p1, const Point &p2) {
ld k1 = p1.angle(), k2 = p2.angle();
return cmp(k1 - k2) ? k1 < k2 : p1.dist() < p2.dist();
}),
build(s2);
}
void build(pair<ld, ld> res[]) {
for (int i = 1; i <= n; ++i) {
int pre = i % n + 1;
ld ang = pt[i].angle() - pt[pre].angle();
if (cmp(ang) < 0)
ang += 2 * M_PI;
res[i] = {pt[i].dist(), ang};
}
}
void getfail() { getfail(s1, kmp1), getfail(s2, kmp2); }
void getfail(pair<ld, ld> s[], int kmp[]) {
for (int i = 2, p = 0; i <= n; ++i) {
while (p && s[p + 1] != s[i])
p = kmp[p];
p = kmp[i] = (s[p + 1] == s[i]) ? p + 1 : p;
}
}
bool match(const Points &pts) const {
if (onf != pts.onf || n != pts.n)
return false;
if (!n)
return true;
return match(pts, s1, kmp1) || match(pts, s2, kmp2);
}
bool match(const Points &pts, const pair<ld, ld> s[], const int kmp[]) const {
int p = 0;
for (int i = 1; i <= pts.n; ++i) {
while (p && !equ(s[p + 1], pts.s1[i]))
p = kmp[p];
if (equ(s[p + 1], pts.s1[i]) && ++p == n)
return true;
}
for (int i = 1; i <= pts.n; ++i) {
while (p && !equ(s[p + 1], pts.s1[i]))
p = kmp[p];
if (equ(s[p + 1], pts.s1[i]) && ++p == n)
return true;
}
return false;
}
} p1, p2;
bool m_ed;
signed main() {
p1.input(1), read(q), p1.getfail();
while (q--) {
p2.input(0);
puts(p1.match(p2) ? "TAK" : "NIE");
}
return 0;
}
|
P3421 Sko
简要题意: 给定 $n$ 个二维向量,求 $2$ 个向量使得它们的整系数线性空间等价于给出的所有向量张成的整系数线性空间。
数据规模: $n \le 100,\ |x|,|y| \le 10^4$。
题解: 倘若能将 $3$ 个向量简化为 $2$ 个,则可以将这 $n$ 个向量都化成 $2$ 个。
考虑向量 $v_1(a_1,b_1),v_2(a_2,b_2),v_3(a_3,b_3)$。在整系数域内,将一个基底加上/减去另一个基底,则张成的线性空间不会改变。因此,可以对向量使用辗转相减法。具体地,对 $v_1$ 和 $v_2$,$v_1$ 和 $v_3$ 依次在 $a$ 这一维辗转相减,可以消去 $a_2,a_3$。此时再对 $v_2$ 和 $v_3$ 在 $b$ 这一维辗转相减,就可以消去 $b_3$。此时 $v_3$ 被消成 $\vec{0}$ 向量,保留 $v_1$ 和 $v_2$ 即可。
此时已经可以在 $O(n \log V)$ 的时间复杂度内解决本题。进一步地,可以发现这个消元过程非常类似线性基。实际上,本题所要维护的就是一个 $2$ 维线性空间的基底。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
template <class _Tp> inline void write(_Tp x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar((x % 10) ^ 48);
}
bool m_be;
using ll = long long;
const int N = 105;
int n, a[N], b[N];
int gcd(int x, int y) { return y ? gcd(y, x % y) : x; }
bool m_ed;
signed main() {
read(n), read(a[1]), read(b[1]);
for (int i = 2; i <= n; ++i) {
read(a[i]), read(b[i]);
while (a[i]) {
if (abs(a[1]) < abs(a[i]))
swap(a[1], a[i]), swap(b[1], b[i]);
else
b[1] -= b[i] * (a[1] / a[i]), a[1] %= a[i];
}
if (i > 2)
b[2] = gcd(b[2], b[i]), b[1] %= b[2];
}
printf("%d %d\n", a[1], b[1]);
printf("%d %d\n", a[2], b[2]);
return 0;
}
|
P3424 Sum
简要题意: 对两个齐肯多夫表示法下的数求和,并以齐肯多夫表示法输出。
数据规模: $n \le 10^6$。
题解: 对题目给定的 $x,y$ 简单相加后,得到的 $z_i \in \{0,1,2\}$。考虑从高位往低位调整。发现 $z_i=2$ 非常麻烦。由于 $0200=0111=1001$,定义一次操作 $op(i)$ 为 $z_{i+1}\leftarrow z_{i+1}+1,z_i\leftarrow z_i-2,z_{i-2}\leftarrow z_{i-2}+1$。将 $z_{i-2}$ 增加到 $3$ 无所谓,因为后面会将低位变为合法,但次操作可能会导致 $z_{i+1}$ 变成 $2$,这是我们所不希望看到的。
考虑 $z_{i+1}$ 会变成 $2$ 的情况,当且仅当 $z_{i+1}=1$ 且 $z_i=2$,那不妨先将 $i$ 这里进位。由于从高到低调整,所以前 $i+1$ 位一定合法,那么 $z_{i+2}=0$。只需要在 $op(i)$ 之前对第 $i$ 位进行进位操作即可。
下面考虑 $z_i=3$ 的情况。前面说过 $op(i)$ 有可能导致 $z_{i-2}$ 变成 $3$。注意到此时由于进行了 $i$ 这里的进位,所以 $z_{i+1}=0$。此时的 $0300$ 经过 $op(i)$ 的变换后得到了 $1101$。由于 $z_{i+2}$ 可能等于 $1$,所以要再对 $i+1$ 进行进位,然后对 $i$ 进位即可。
说了这么多,其实最终的做法也很简单($flush(i)$ 表示对 $i$ 进位):
- 从高到低位枚举 $i$。
- $flush(i)$。
- 若 $z_i\ge 2$,则依次进行 $op(i),flush(i+1),flush(i)$。
分析一下复杂度。对于加法操作,进位的复杂度是均摊的,所以总复杂度位线性。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
template <class _Tp> inline void write(_Tp x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar((x % 10) ^ 48);
}
bool m_be;
using ll = long long;
const int N = 1e6 + 10;
int n, m, a[N];
void flush(int p) {
while (a[p] && a[p + 1])
++a[p + 2], --a[p], --a[p + 1], p += 2;
}
bool m_ed;
signed main() {
read(n);
for (int i = 1; i <= n; ++i)
read(a[i]);
read(m);
for (int i = 1, x; i <= m; ++i)
read(x), a[i] += x;
n = max(n, m) + 2;
for (int i = n; i >= 1; --i) {
flush(i);
if (a[i] >= 2) {
if (i >= 2)
a[i] -= 2, ++a[i + 1], ++a[max(1, i - 2)];
else
a[i] -= 2, ++a[i + 1];
flush(i + 1), flush(i);
}
}
while (n && !a[n])
--n;
write(n), putchar(' ');
for (int i = 1; i <= n; ++i)
write(a[i]), putchar(" \n"[i == n]);
return 0;
}
|
P3425 Kos
简要题意: $n$ 个人玩 $m$ 场游戏,每局游戏 $2$ 个人玩,求赢的次数最多的人至少赢了多少次。
数据规模: $n,m \le 10^4$。
题解: 显然外层二分答案 $ans$。考虑如何判断,每局游戏只有 $2$ 种结果,分别是 $a$ 赢和 $b$ 赢。考虑使用网络流,建模如下:
- 源点 $s$ 连向每个人 $i$,流量为 $ans$
- 对每个游戏新建点 $p$,连 $a\to p$ 和 $b\to p$,流量 $1$
- 每个游戏的点 $p\to t$,流量 $1$
判断是否最大流为 $m$ 即可。复杂度跑不满的 $O(n \sqrt n \log n)$,因为是二分图。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
template <class _Tp> inline void write(_Tp x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar((x % 10) ^ 48);
}
bool m_be;
using ll = long long;
const int N = 1e4 + 10;
int n, m, eu[N], ev[N];
bool ansp[N];
namespace flow {
const int N = 2e4 + 10, M = 4e4 + 10;
struct Edge {
int v, f, nxt;
} e[M * 2];
int n, s, t, etot, head[N], cur[N], lev[N];
void clear(int m) {
n = m + 2, s = m + 1, t = m + 2, etot = 1;
fill(head + 1, head + n + 1, 0);
}
void addedge(int u, int v, int f) {
e[++etot] = {v, f, head[u]}, head[u] = etot;
e[++etot] = {u, 0, head[v]}, head[v] = etot;
}
bool bfs() {
queue<int> que;
fill(lev + 1, lev + n + 1, -1);
que.push(s), lev[s] = 0;
while (!que.empty()) {
int u = que.front();
que.pop();
for (int i = cur[u] = head[u]; i; i = e[i].nxt)
if (e[i].f && lev[e[i].v] == -1)
lev[e[i].v] = lev[u] + 1, que.push(e[i].v);
}
return lev[t] != -1;
}
int dfs(int u, int mx) {
if (u == t || !mx)
return mx;
int ret = 0;
for (int &i = cur[u]; i; i = e[i].nxt) {
if (lev[e[i].v] != lev[u] + 1)
continue;
int tmp = dfs(e[i].v, min(mx, e[i].f));
e[i].f -= tmp, e[i ^ 1].f += tmp;
mx -= tmp, ret += tmp;
if (!mx)
break;
}
return ret;
}
int flow() {
int ret = 0;
while (bfs())
ret += dfs(s, 1e9);
return ret;
}
} // namespace flow
bool check(int k) {
flow::clear(n + m);
for (int i = 1; i <= n; ++i)
flow::addedge(flow::s, i, k);
for (int i = 1; i <= m; ++i) {
flow::addedge(eu[i], n + i, 1e9);
flow::addedge(ev[i], n + i, 1e9);
flow::addedge(n + i, flow::t, 1);
}
return flow::flow() == m;
}
bool m_ed;
signed main() {
read(n), read(m);
for (int i = 1; i <= m; ++i)
read(eu[i]), read(ev[i]);
int l = 0, r = m, ans = m;
while (l <= r) {
int mid = (l + r) >> 1;
if (check(mid)) {
r = mid - 1, ans = mid;
} else {
l = mid + 1;
}
}
write(ans), putchar('\n'), check(ans);
for (int p = 1; p <= m; ++p)
for (int i = flow::head[p + n]; i; i = flow::e[i].nxt)
if (flow::e[i].v != flow::t && flow::e[i].f)
ansp[p] = (flow::e[i].v == eu[p]);
for (int i = 1; i <= m; ++i)
write(ansp[i]), putchar('\n');
return 0;
}
|
P3426 Sza
简要题意: 给定长度为 $n$ 的字符串,求最短的串的使得可以用若干个可以相交的该串形成原串,且相交的部分必须相同。
数据规模: $n \le 5\times 10^5$。
题解: 显然这个串得同时是原串的前缀和后缀,否则一定无法形成原串。
设 $dp_i$ 表示形成 $[1,i]$ 的前缀所需的最短串长。考察 $dp_i$ 可能的取值,必然有 $s[1,dp_i]$ 与 $s[i-dp_i+1,i]$ 相同,这让人想到 kmp。进一步地,发现 $dp_i$ 只可能是 $i$ 或 $dp_{fail_i}$,故考虑什么情况下可以从 $dp_{fail_i}$ 进行转移。
不妨将前缀 $[1,i]$ 划分为 $[1,i-fail_i]$ 与 $[i-fail_i+1, i]$ 两个部分,后者的答案显然等价于 $dp_{fail_i}$。于是,若存在 $j \ge i - fail_i$ 使得 $dp_j = dp_{fail_i}$,即 $dp_i \leftarrow dp_{fail_i}$。
具体实现,用桶记录一下每个 $dp=i$ 的最大的 $i$ 即可做到线性。
启示: 自己第一遍做的时候,总是在想着用 kmp 的树形结构,从而对每个长度的前缀都分别判断是否合法。但对于很多字符串题,包括许多经典的字符串算法,都是对已知的信息进行重复利用,例如本题就在求 $dp_i$ 的值时对 $dp_{fail_i}$ 进行了重复利用。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| #include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
int n, dp[N], kmp[N], buc[N];
char str[N];
signed main() {
scanf("%s", str + 1);
n = strlen(str + 1);
for (int i = 2, p = 0; i <= n; ++i) {
while (p && str[i] != str[p + 1])
p = kmp[p];
p = kmp[i] = (str[i] == str[p + 1] ? p + 1 : p);
}
for (int i = 1; i <= n; ++i)
dp[i] = (buc[dp[kmp[i]]] >= i - kmp[i]) ? dp[kmp[i]] : i, buc[dp[i]] = i;
return printf("%d\n", dp[n]), 0;
}
|
P3427 Dzi
简要题意: 给一张无向图,将点排布在 $2$ 条平行的直线上,使得没有两个点在同一位置,同一条直线上的点之间没有边,且点之间连的边所形成的线段不交。问方案数,对给定的模数取模。
数据规模: $n \le 10^6,\ m \le 5,400,000,\ p \le 2\times 10^6$。
题解: 显然这张图必须得是二分图,进一步研究发现如果有环也不可以,所以合法的图形成了一棵森林。考虑合法的森林的形态,如果有一个点同时连接了 $> 2$ 个度数 $\ge 2$ 的点则也不合法。容易证明其他图的形态均合法,于是合法的图一定由若干 “毛毛虫” 形状的连通块构成,其中 “躯干” 为若干度数 $\ge 2$ 的点所构成的链,而 “触角” 则是从 “躯干” 处延伸出来的度数为 $1$ 的点。
考虑如何统计方案数。各连通块之间互不影响,所以只考虑当前连通块的方案数。同一组 “触角” 可以任意排列,方案数是触角数量的阶乘的乘积;躯干显然需要一左一右地分布在 $2$ 条直线上,可以对连通块进行上下/左右翻转,乘上 $4$ 的系数即可。
实现细节较多,如躯干长度为 $1$ 的毛毛虫不需要上下翻转,孤立点可以插空放在任意位置等,写的时候需要非常仔细。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
template <class _Tp> inline void write(_Tp x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar((x % 10) ^ 48);
}
bool m_be;
using ll = long long;
const int N = 1e6 + 10;
int n, m, mod, fac[N], deg[N], col[N], fdeg[N];
bool vis[N];
vector<int> g[N], vec[2], dvec;
void dfs(int u, int c) {
col[u] = c, vec[c].push_back(u);
for (auto v : g[u]) {
if (col[v] == c)
puts("0"), exit(0);
if (col[v] == -1)
dfs(v, !c);
}
}
bool m_ed;
signed main() {
read(n), read(m), read(mod), fac[0] = 1;
for (int i = 1; i <= n; ++i)
fac[i] = 1ll * fac[i - 1] * i % mod;
for (int i = 1; i <= m; ++i) {
int u, v;
read(u), read(v), ++deg[u], ++deg[v];
g[u].push_back(v), g[v].push_back(u);
}
for (int u = 1; u <= n; ++u) {
if (deg[u] < 2)
continue;
for (auto v : g[u])
if (deg[v] >= 2)
++fdeg[u];
if (fdeg[u] > 2)
puts("0"), exit(0);
}
int ans = 1, kcnt = 0, ocnt = 0;
fill(col + 1, col + n + 1, -1);
for (int s = 1; s <= n; ++s) {
if (col[s] != -1)
continue;
vec[0].clear(), vec[1].clear(), dfs(s, 0);
int scnt = vec[0].size() + vec[1].size();
++kcnt;
if (scnt == 1) {
++ocnt, --kcnt;
continue;
}
if (scnt == 2) {
ans = ans * 2 % mod;
continue;
}
dvec.clear(), dvec.resize(1), dvec[0] = 0;
for (auto p : vec[0])
if (deg[p] >= 2 && fdeg[p] <= 1)
dvec[0] = p;
for (auto p : vec[1])
if (deg[p] >= 2 && fdeg[p] <= 1)
dvec[0] = p;
if (!dvec[0])
puts("0"), exit(0);
for (int u = dvec[0], p = 0, nxt = 0; u; p = u, u = nxt, nxt = 0) {
if (u != dvec[0])
dvec.push_back(u);
for (auto v : g[u])
if (deg[v] >= 2 && v != p)
nxt = v;
}
int cur = (dvec.size() > 1) ? 4 : 2;
for (auto p : dvec)
cur = 1ll * cur * fac[deg[p] - fdeg[p]] % mod;
ans = 1ll * ans * cur % mod;
}
ans = 1ll * ans * fac[kcnt] % mod;
for (int i = n - ocnt + 2; i < n + 2; ++i)
ans = 1ll * ans * i % mod;
return write(ans), putchar('\n'), 0;
}
|
P3428 Akc
简要题意: 给定 $n$ 个圆,求最小的 $i$ 使得前 $i$ 个圆的交集为空。
数据规模: $n \le 2000$。
题解: 需要维护圆的交集是否存在,可以接受的复杂度为 $O(n^2)$ 级别的。
注意到由于圆是凸的,所以若干个圆的交集也是凸的。对于图形的交是否为空,只需要判断 “交集” 的顶点中的一个代表点是否被所有图形包含。对于本题,取 “交集” 中 $x$ 坐标最大的顶点作为代表点,判断其是否在所有圆内即可。
现在问题转化为如何求出若干圆的交集中 $x$ 坐标最大的顶点,根据交集的意义,容易证明就是圆两两交集的代表顶点中 $x$ 坐标最小的那个,于是问题变成了求两个圆的交点坐标。
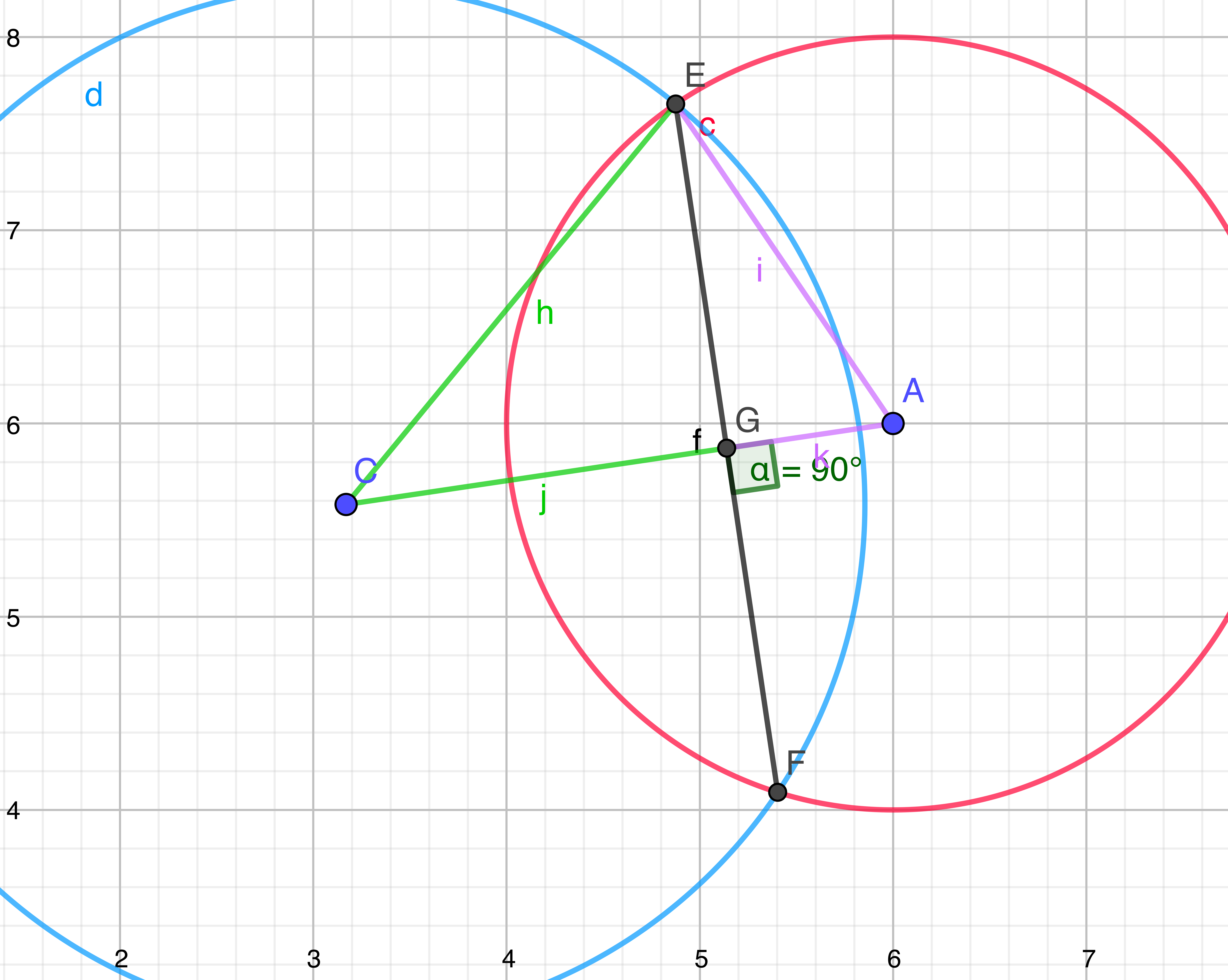
如上图所示,我们只需求出 $G$ 的坐标以及向量 $\vec{GE}$ 即可得到点 $E,F$ 的坐标。而 $G$ 的坐标可以用向量 $\vec{AC}$ 乘上 $\frac{AG}{AC}$ 再加上向量 $OA$ 求得;$AC \bot GE$,因此只要求出 $|GE|$ 即可得到 $\vec{GE}$。假设 $AG=x,GE=h$,则可以根据勾股定理列出方程求解。具体方程就不再列出来了,也就是小学生都会做的水平。
于是圆的交点便能够 $O(1)$ 求出,而 $n$ 个圆是否有交便可以 $O(n^2)$ 进行判断了(并支持在线!),从小到大枚举 $i$ 并计算前 $i$ 个圆的交即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
bool m_be;
using ll = long long;
const int N = 2e3 + 10;
const double eps = 1e-10;
int n;
inline int cmp(const double &v) {
if (abs(v) <= eps)
return 0;
return v < 0 ? -1 : 1;
}
inline double sqr(const double &v) { return v * v; }
struct Point {
double x, y;
Point operator+(const Point &p) const { return {x + p.x, y + p.y}; }
Point operator-(const Point &p) const { return {x - p.x, y - p.y}; }
Point operator*(const double &k) const { return {x * k, y * k}; }
double dist() const { return hypot(x, y); }
};
struct Circle {
Point o;
double r;
Point getr() const { return {o.x + r, o.y}; }
bool contains(const Point &p) const { return cmp((p - o).dist() - r) <= 0; }
} cir[N];
inline bool empty(const Point &p) { return isnan(p.x) || isnan(p.y); }
inline Point getpt(const Circle &cira, const Circle &cirb) {
double d = (cira.o - cirb.o).dist();
if (cmp(d - cira.r - cirb.r) == 1)
return {nan(""), nan("")};
if (cmp(cira.r - cirb.r - d) >= 0)
return cirb.getr();
if (cmp(cirb.r - cira.r - d) >= 0)
return cira.getr();
if (cira.contains(cirb.getr()))
return cirb.getr();
if (cirb.contains(cira.getr()))
return cira.getr();
double ra = sqr(cira.r), rb = sqr(cirb.r);
double a = (ra + sqr(d) - rb) / (d * 2);
double h = sqrt(sqr(cira.r) - sqr(a));
Point mid = cira.o + (cirb.o - cira.o) * (a / d);
Point add = Point{cirb.o.y - cira.o.y, cira.o.x - cirb.o.x} * (h / d);
Point p1 = mid + add, p2 = mid - add;
return (cmp(p1.x - p2.x) < 0 ? p2 : p1);
}
bool m_ed;
signed main() {
scanf("%d", &n);
for (int i = 1; i <= n; ++i)
scanf("%lf%lf%lf", &cir[i].o.x, &cir[i].o.y, &cir[i].r);
Point pt = {1e9, 1e9};
for (int i = 1; i <= n; ++i) {
if (i == 2) {
pt = getpt(cir[1], cir[2]);
} else if (i > 2) {
for (int j = 1; !empty(pt) && j < i; ++j) {
Point tmp = getpt(cir[i], cir[j]);
if (empty(tmp) || tmp.x < pt.x)
pt = tmp;
}
for (int j = 1; !empty(pt) && j <= i; ++j)
if (!cir[j].contains(pt))
pt = {nan(""), nan("")};
}
if (empty(pt))
return printf("%d\n", i), 0;
}
return puts("NIE"), 0;
}
|
P3429 Dwa
简要题意: 将一张无向图的点分成两个集合,去掉所有跨越集合的边,使得尽量多的点度数为偶数,输出分到其中一个集合中的所有点。
数据规模: $n \le 200$。
题解: ~~(有论文)~~可以证明一定有方法使得一张图被划分为 $2$ 部分,每个部分的生成子图中点度数都为偶数。这里不再赘述。
定义变量 $x_i \in [0,1]$ 表示划分后 $i$ 所在的集合。不难发现可以得到一下方程组:
$$
\forall u,\mathop\oplus_{(u,v)\in \rm E} (x_u \oplus x_v \oplus 1) = 0
$$
使用高斯消元求解该方程组即可。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
template <class _Tp> inline void write(_Tp x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar((x % 10) ^ 48);
}
bool m_be;
using ll = long long;
const int N = 205;
int n;
bitset<N> a[N], ans;
bool m_ed;
signed main() {
read(n);
for (int i = 1; i <= n; ++i) {
int k, x;
read(k);
while (k--)
read(x), a[i][x] = 1, a[i][i].flip(), a[i][n + 1].flip();
}
for (int i = 1; i <= n; ++i) {
for (int j = i + 1; j <= n; ++j)
if (a[j][i]) {
swap(a[i], a[j]);
break;
}
if (!a[i][i])
continue;
for (int j = i + 1; j <= n; ++j)
if (a[j][i])
a[j] ^= a[i];
}
vector<int> vec;
for (int i = n; i >= 1; --i) {
if (!a[i][i])
continue;
ans[i] = ((ans & a[i]).count() & 1) ^ a[i][n + 1];
if (ans[i])
vec.push_back(i);
}
write(vec.size()), putchar('\n');
for (int i = 0; i < (int)vec.size(); ++i)
write(vec[i]), putchar(" \n"[i == (int)vec.size() - 1]);
return 0;
}
|
P3433 Pra
简要题意: 给定平面上 $n$ 个点,一个人从点 $1$ 开始走,一开始面向点 $2$,每次只能在点上转向且只能向右转 $\le 180^\circ$。问在路线不交叉的情况下回到点 $1$ 最多可以经过多少个点。
数据规模: $n \le 1000$。
题解: 先令点 $1$ 为坐标原点。由于只能向右转且路线不能交叉,所以围成的图形除了在点 $1$ 可能会凹进去之外都是凸的。进一步发现若将其他点按照极角排序,则经过的点按照极角有序(显然)。
于是可以进行 dp。设 $dp_{i,j}$ 表示当前在点 $i$,上一个经过的点为 $j$,所经过的最长距离。转移时暴力枚举下一个点的位置并更新 $dp$ 值,这样做是 $O(n^3)$ 的,无法接受。
直接优化并不容易,但接下来便是很妙的一步,可以交换 dp 的某一维和 dp 值。重新设 $dp_{i,j}$ 表示当前在点 $i$,经过的最长距离为 $j$ 时,使得接下来可走的范围最大的上一个点。这样可以整体计算 dp,枚举上一个点并二分 $j$ 这一维以修改当前的 $dp$ 值。
这样的复杂度是 $O(n^2 \log n)$,为了确保精度可以用叉积进行比较。
启示: 在 dp 状态很难继续优化的时候,如果 dp 值的范围不大,可以尝试交换值某一维。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| #include <bits/stdc++.h>
using namespace std;
#define resetIO(x) \
freopen(#x ".in", "r", stdin), freopen(#x ".out", "w", stdout)
#define debug(fmt, ...) \
fprintf(stderr, "[%s:%d] " fmt "\n", __FILE__, __LINE__, ##__VA_ARGS__)
template <class _Tp> inline _Tp &read(_Tp &x) {
bool sign = false;
char ch = getchar();
for (; !isdigit(ch); ch = getchar())
sign |= (ch == '-');
for (x = 0; isdigit(ch); ch = getchar())
x = x * 10 + (ch ^ 48);
return sign ? (x = -x) : x;
}
template <class _Tp> inline void write(_Tp x) {
if (x < 0)
putchar('-'), x = -x;
if (x > 9)
write(x / 10);
putchar((x % 10) ^ 48);
}
bool m_be;
using ll = long long;
const int N = 1e3 + 10;
int n, dp[N][N];
struct Point {
int x, y;
Point operator+(const Point &p) const { return {x + p.x, y + p.y}; }
Point operator-(const Point &p) const { return {x - p.x, y - p.y}; }
int operator*(const Point &p) const { return x * p.y - y * p.x; }
} pt[N];
bool m_ed;
signed main() {
read(n);
for (int i = 1; i <= n; ++i)
read(pt[i].x), read(pt[i].y);
for (int i = 2; i <= n; ++i)
pt[i] = pt[i] - pt[1];
sort(pt + 3, pt + n + 1, [&](const auto &x, const auto &y) {
int cx = pt[2] * x, cy = pt[2] * y;
if ((cx > 0) != (cy > 0))
return cx < 0;
return x * y < 0;
});
int ans = 1;
dp[2][1] = dp[2][2] = 1;
for (int i = 3; i <= n; ++i) {
for (int j = 2; j < i; ++j) {
if (pt[i] * pt[j] < 0)
continue;
int l = 1, r = j, pos = -1;
while (l <= r) {
int mid = (l + r) >> 1;
if (!dp[j][mid] || (pt[j] - pt[dp[j][mid]]) * (pt[i] - pt[j]) > 0) {
r = mid - 1;
} else {
l = mid + 1, pos = mid;
}
}
if (pos == -1)
continue;
ans = max(ans, pos);
if (!dp[i][pos + 1] || (pt[i] - pt[j]) * (pt[i] - pt[dp[i][pos + 1]]) < 0)
dp[i][pos + 1] = j;
}
for (int j = i - 1; j >= 1; --j) {
if (!dp[i][j + 1])
continue;
if (!dp[i][j] || (pt[i] - pt[dp[i][j + 1]]) * (pt[i] - pt[dp[i][j]]) < 0)
dp[i][j] = dp[i][j + 1];
}
}
return write(ans), putchar('\n'), 0;
}
|
最后修改于 2025-07-05
Git 版本:
de2abab
